Statistik für die medizinische Dissertation / Seite 1
Dr. Susann Wolff, Daniela Keller
Statistik ist ein wichtiger Teil vieler Dissertationen in der Medizin. Wie Statistik dabei richtig angewandt wird, welche Methoden sich bewährt haben und wie Sie zu Ergebnissen kommen, erläutert dieser Text.
Abb. 1: Aufbau der Datenanalyse, aus J. Webinger, D. Keller, B. Budrich: Wie schreibe ich eine Doktorarbeit? Leitfaden für Mediziner und Zahnmediziner. Springer 2014.
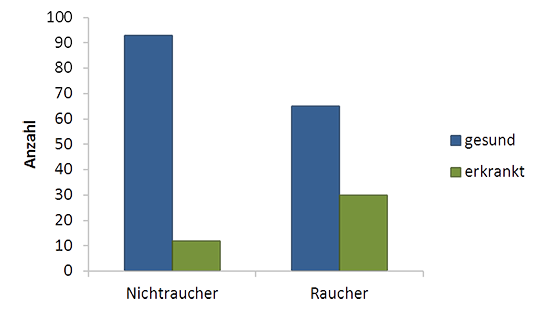
Abb. 2: Gruppiertes Balkendiagramm zur Darstellung kategorialer Daten. Kategoriale Variablen: Rauchen (nein/ja), Erkrankung (nein/ja). Die Höhe der Balken zeigt die Anzahl der Personen in den jeweiligen Kategorien.
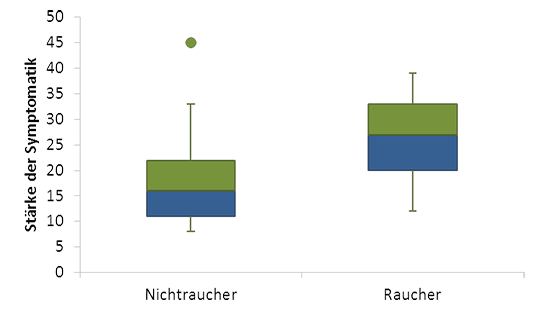
Abb. 3: Boxplots zur Darstellung metrischer Daten. Abhängige metrische Variable: Stärke der Symptomatik (Skala von 0 bis 50), unabhängige kategoriale Variable: Rauchen (nein/ja). Die Unterteilungslinie innerhalb der Boxen zeigt den Median, die Länge der Boxen zeigt den IQR, die Endpunkte der Antennen („Whisker“) zeigen Minimum und Maximum, der Kreis zeigt einen Ausreißer.
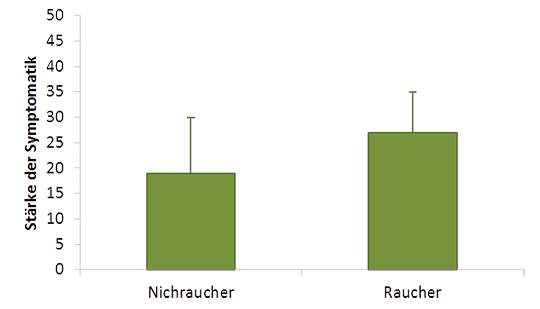
Abb. 4: Balkendiagramme zur Darstellung metrischer Daten. Abhängige metrische Variable: Stärke der Symptomatik (Skala von 0 bis 50), unabhängige kategoriale Variable: Rauchen (nein/ja). Die Höhe der Balken zeigt die Mittelwerte der zwei Stichprobengruppen, die Fehlerbalken zeigen die Standardabweichungen.
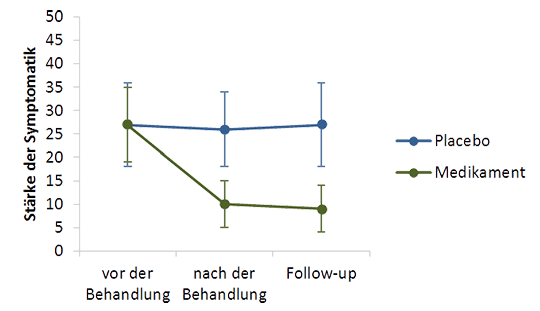
Abb. 5: Liniendiagramme zur Darstellung metrischer Daten. Abhängige metrische Variable: Stärke der Symptomatik (Skala von 0 bis 50), unabhängige kategoriale Variablen: Behandlung (Placebo/Medikament), Zeitpunkt (vor der Behandlung/nach der Behandlung/Follow-up-Messung). Die Punkte zeigen die Mittelwerte der zwei Gruppen zu den drei Zeitpunkten, die Fehlerbalken zeigen die Standardabweichungen.
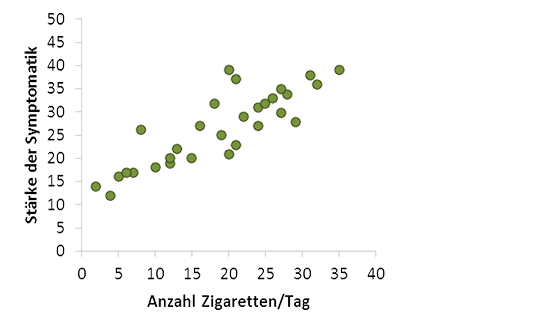
Abb. 6: Streudiagramm zur Darstellung metrischer Daten. Metrische Variablen: Stärke der Symptomatik (Skala von 0 bis 50), Anzahl Zigaretten pro Tag (Skala von 0 bis 40). Jeder Punkt entspricht einem einzelnen Probanden und zeigt dessen Werte auf den beiden metrischen Skalen.
Weiterlesen: Statistik für medizinische Dissertationen / Seite 2